While discussing game scripting languages with a friend, I asserted that a Lisp-based language such as Scheme or Racket would form a very effective in-game scripting language due to its expressive power and flexibility, as well as the efficiency with which modern, JIT-capable implementations execute code. One of the most widely used scripting languages for this purpose appears to be Lua which is pretty small and designed to be embedded in C programs. I glanced over the feature list on Wikipedia and saw that it was basically a subset of Scheme with some omissions and a few additions. In particular, I really liked the idea of a metatable, which effectively automatically handled function memoization.
The example given on Wikipedia is a metatable-based function to calculate the nth Fibonacci number, a classic example of a simple recursive expression that has exponential time complexity for a naïve implementation, but can be improved to linear time (or, depending on the usage scenario, amortized constant time, for sufficient reuse) with a memoization table. The Lua for this is given (available under the Creative Commons Attribution-ShareAlike license from Wikipedia as:
fibs = { 1, 1 }
setmetatable(fibs, {
__index = function(name, n)
name[n] = name[n - 1] + name[n - 2]
return name[n]
end
})
I didn't recall seeing a Scheme or Racket built-in to provide the same functionality, but I was confident that it would be easy to implement such a language feature using standard Racket built-ins, such as the hash table. So, I started with a simple function that would check if a value for 'arg' existed in a given hash table, and if so, return that value, otherwise compute a value by applying the given function, storing the result, and then returning:
(define (memo-or-call ht fun arg)
(if (hash-has-key? ht arg)
(hash-ref ht arg)
(let ((result (fun arg)))
(hash-set! ht arg result)
result)))
With this, I was able to define a hash table on my own, set up the default values, and then create an index function, which was pretty effective and enabled me to compute any Fibonacci number that I wanted almost instantly:
(define fibtable (make-hash))
(hash-set! fibtable 0 1)
(hash-set! fibtable 1 1)
(define (fib n)
(memo-or-call fibtable
(lambda (k) (+ (fib (- k 1)) (fib (- k 2))))
n))
This is great, but it felt like it required too much template-like rewriting of code for each function that I wanted to provide table memoization for. I'd have to create a new hash table, add default values, and then use the "internal" function memo-or-call to create my memoization-capable function. To resolve this, I wrote another function that would take a lambda expression and wrap it with a hash table and call to the memoization function:
(define (mt-store-defaults tbl defaults)
(cond
[(empty? defaults) tbl]
[else (hash-set! tbl (caar defaults) (cadar defaults))
(mt-store-defaults tbl (cdr defaults))]))
(define (make-metatable fun defaults)
(let ((tbl (mt-store-defaults (make-hash) defaults)))
(lambda (k)
(memo-or-call tbl fun k))))
This reduced the complexity of creating a new memorized function considerably, which brought me to
functionality that was effectively equivalent to what was possible in Lua. It's worth noting that
I'm strictly dealing with the case where a table is used to memorize computation; not the
other usage cases, such as implementing classes or objects, although it would be possible to modify
the idea here to include support for the __call magic function in Lua,
and it is already possible to store functions in a hash table, as they are still first class
objects. Scheme code implementing the now-table-based Fibonacci calculator
(define fib2
(make-metatable
(lambda (k) (+ (fib2 (- k 1)) (fib2 (- k 2))))
'((0 1) (1 1))))
Therefore, in summary, a reasonable implementation of automatic memoization with "metatables" can be achieved with just a few lines of Scheme/Racket, allowing for concise definitions of memorized functions in user code. Note that this is just some example code and not really robust, but feel free to use it as a starting point.
#lang racket
(define (memo-or-call ht fun arg)
(if (hash-has-key? ht arg)
(hash-ref ht arg)
(let ((result (fun arg)))
(hash-set! ht arg result)
result)))
(define (mt-store-defaults tbl defaults)
(cond
[(empty? defaults) tbl]
[else (hash-set! tbl (caar defaults) (cadar defaults))
(mt-store-defaults tbl (cdr defaults))]))
(define (make-metatable fun defaults)
(let ((tbl (mt-store-defaults (make-hash) defaults)))
(lambda (k)
(memo-or-call tbl fun k))))

 represents resistance total,
represents resistance total,  represents armor total,
represents armor total,  represents the monster level
(60 for all of inferno, as far as I can tell), and
represents the monster level
(60 for all of inferno, as far as I can tell), and  is the reduction, which is expressed on the
UI as a percentage. Therefore
is the reduction, which is expressed on the
UI as a percentage. Therefore  is used to calculate how much damage is done by an attack. The
two resistances multiply, so the total damage done by a single attack is given as $
(1-r{resist})(1-r{armor})$ multiplied by the initial attack damage. Note that if you find a shrine
of protection or use a skill such as the wizard's blur ability, it is counted in a third category
that we will ignore from here out. This category is multiplied in exactly the same way, so total
damage becomes
is used to calculate how much damage is done by an attack. The
two resistances multiply, so the total damage done by a single attack is given as $
(1-r{resist})(1-r{armor})$ multiplied by the initial attack damage. Note that if you find a shrine
of protection or use a skill such as the wizard's blur ability, it is counted in a third category
that we will ignore from here out. This category is multiplied in exactly the same way, so total
damage becomes  in that case.
in that case.
 by 10/10, we will get the same expression that is used to find the
reduction by armor, which suggests that 1 resistance to all is equal to 10 armor because they
increase their respective reductions at the same rate. This is only accurate in certain cases,
because the total damage reduction depends on the product of all resistance and armor, rather than a
linear combination of the two.
by 10/10, we will get the same expression that is used to find the
reduction by armor, which suggests that 1 resistance to all is equal to 10 armor because they
increase their respective reductions at the same rate. This is only accurate in certain cases,
because the total damage reduction depends on the product of all resistance and armor, rather than a
linear combination of the two.


 and
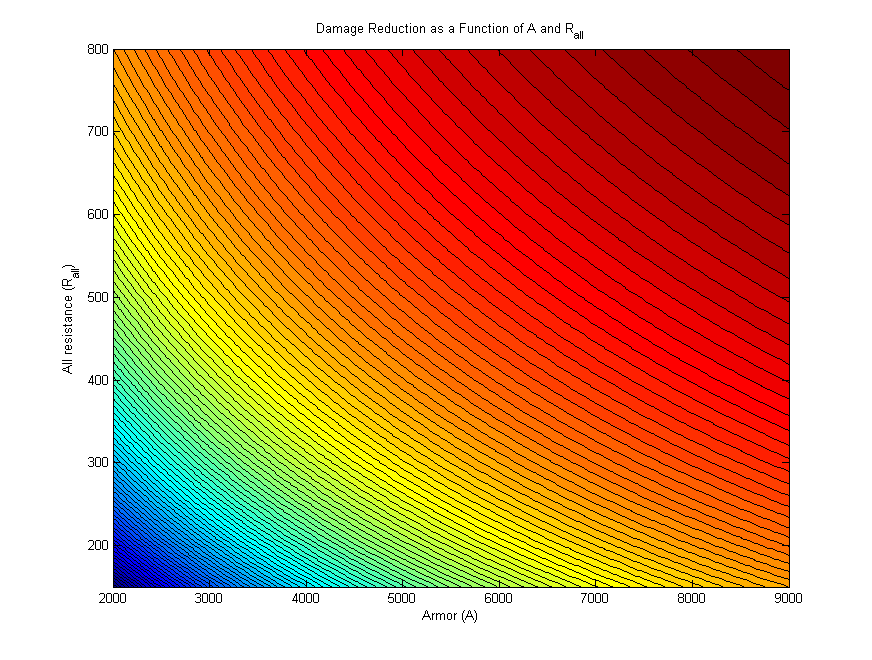
and  are equal. This is kind of hard to visualize, so it's much more useful to simply
create a contour plot of damage reduction as a function of both armor and all resistance, which
serves as a guide for the relationship between the two stats.
are equal. This is kind of hard to visualize, so it's much more useful to simply
create a contour plot of damage reduction as a function of both armor and all resistance, which
serves as a guide for the relationship between the two stats.