I normally don't write about videogames, but I thought it would be fun to take some time to write about the armor and resistance system in Diablo III, as well as to throw some math at it to see how best to improve one's character.
In Diablo III, the key to surviving Inferno is getting appropriate gear. However, aside from the obvious improvements of increasing the stats on an item, it can be difficult to intuitively judge the tradeoffs between dissimilar stats. Is it worth it to give up 40 vitality points in order to gain 20 points of resistance to all? How about trading 100 points of strength for 100 points of intelligence? In trying to answer these questions, we will temporarily ignore the question of damage, because, if you can't survive an attack from an Inferno-level elite, unless you do over a million DPS, you won't have a chance to kill it anyway. There are two basic concepts to understanding survivability when absorbing damage (we will ignore dodge because it further complicates things): damage reduction and effective hit points, which are really two ways of looking at the same stats.
Damage Reduction
The combat system is pretty straightforward: when a monster attacks, a random number is generated between its min and max attack values, that number is reduced by armor, resistance, and extra modifiers, and then the resulting value is subtracted from your health. The consensus (which can be experimentally verified) is that the resistance and armor reductions can be found with the following formulas:

Where  represents resistance total,
represents resistance total,  represents armor total,
represents armor total,  represents the monster level
(60 for all of inferno, as far as I can tell), and
represents the monster level
(60 for all of inferno, as far as I can tell), and  is the reduction, which is expressed on the
UI as a percentage. Therefore
is the reduction, which is expressed on the
UI as a percentage. Therefore  is used to calculate how much damage is done by an attack. The
two resistances multiply, so the total damage done by a single attack is given as $
(1-r{resist})(1-r{armor})$ multiplied by the initial attack damage. Note that if you find a shrine
of protection or use a skill such as the wizard's blur ability, it is counted in a third category
that we will ignore from here out. This category is multiplied in exactly the same way, so total
damage becomes
is used to calculate how much damage is done by an attack. The
two resistances multiply, so the total damage done by a single attack is given as $
(1-r{resist})(1-r{armor})$ multiplied by the initial attack damage. Note that if you find a shrine
of protection or use a skill such as the wizard's blur ability, it is counted in a third category
that we will ignore from here out. This category is multiplied in exactly the same way, so total
damage becomes  in that case.
in that case.
The reduction is the remainder after the damage amount is subtracted from the total damage. If we normalize by the monster's damage, we find that the damage reduction for any attack becomes:

To increase one's survivability, it is necessary to increase the value of damage reduction, but
because stats are limited on items, there is always a tradeoff. Because there is a direct,
unchanging relationship between strength an armor (1 strength adds 1 armor) and between intelligence
and resistance to all (10 intelligence adds 1 to all resistance), we will first look at the
tradeoff between armor and resistance alone. A quick look at the two equations tells us that if we
multiply  by 10/10, we will get the same expression that is used to find the
reduction by armor, which suggests that 1 resistance to all is equal to 10 armor because they
increase their respective reductions at the same rate. This is only accurate in certain cases,
because the total damage reduction depends on the product of all resistance and armor, rather than a
linear combination of the two.
by 10/10, we will get the same expression that is used to find the
reduction by armor, which suggests that 1 resistance to all is equal to 10 armor because they
increase their respective reductions at the same rate. This is only accurate in certain cases,
because the total damage reduction depends on the product of all resistance and armor, rather than a
linear combination of the two.
Instead, it is much more useful to examine the partial derivatives of damage reduction with respect to all resistance and armor, respectively:


The partial derivative of damage reduction due to all resistance can be found analogously to be:

The relationship between all resistance and armor is, therefore, dependent on what the two values
are, and we can see that increasing the smaller value will have a larger impact on total damage
reduction than further increasing the larger value will, which means that 1 all resistance is not
always worth the same as 10 armor, when it comes to changing damage reduction—sometimes all
resistance is more valuable, and sometimes less, with the 1:10 ratio being equal when  and
and  are equal. This is kind of hard to visualize, so it's much more useful to simply
create a contour plot of damage reduction as a function of both armor and all resistance, which
serves as a guide for the relationship between the two stats.
are equal. This is kind of hard to visualize, so it's much more useful to simply
create a contour plot of damage reduction as a function of both armor and all resistance, which
serves as a guide for the relationship between the two stats.
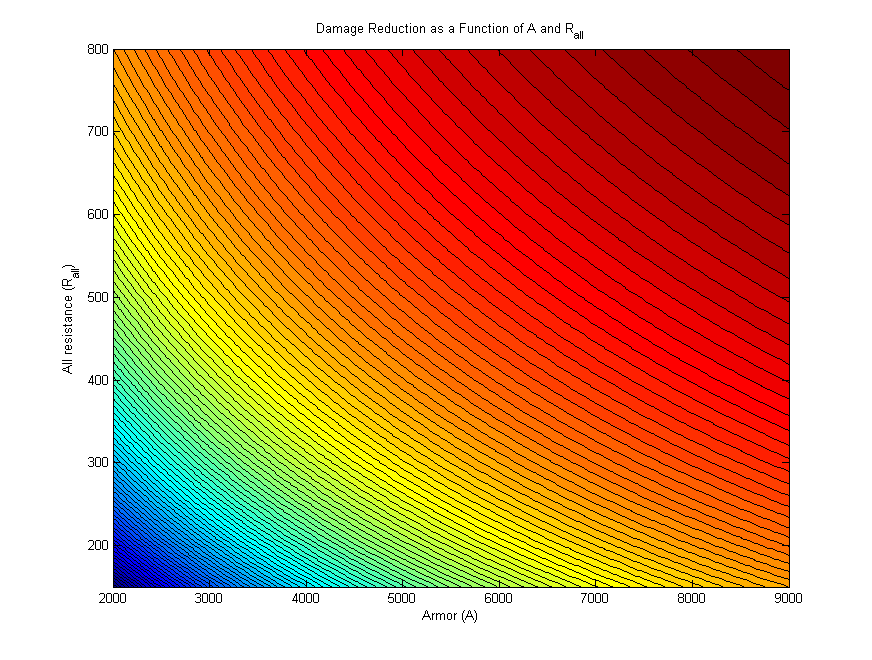
Moving to a darker red area represents an increase in total damage reduction, and so we see that along the diagonal, both contribute equally, but when one variable is significantly larger than the other, further increases are not as effective as bumping the lower stat would be.
Effective HP
With a good understanding of how damage resistance is calculated, it is time to extend the concept to allow us to include other tradeoffs when determining which gear to use. The next component of survivability is how many hit points your character has. However, all characters with 30,000 HP are not created equal—the character with better damage reduction will do better in combat, so our goal is to quantify the relationship between hit points and damage reduction.
In order to compare characters with different resistances and HP, it is necessary to eliminate the armor and resistance entirely and focus on only a single point of comparison that summarizes the effects of all of the attributes, which is known as 'Effective HP.' If a character with 90% damage reduction is hit and suffers 10,000 HP worth of damage, by inverting the equation we can find that the attack must have done 100,000 HP of damage originally, and so, an equivalent character with zero armor and zero resist would have an effective 100k HP for each 10k HP that our character has. The direct formula for effective HP from actual HP and damage reduction is:

At this point, more derivatives could be calculated to find the effects of changing vitality, armor, or resistance on effective HP, but it is much simpler to create a spreadsheet that computes the effective HP for a given triple of vitality (plus your character's base hit points, which is not zero), armor, and all resistance, and then using that to compare different gear setups. Intuitively, more effective HP is better, as it means you will survive longer against elites and champions, regardless of whether your actual HP increased or decreased. The same is true for your damage reduction; your effective HP can increase despite damage reduction decreasing, if your base HP is sufficiently increased at the same time. It is also worth noting that all HP regeneration becomes more effective as damage reduction goes up—the effective HP regeneration can be calculated in exactly the same way as effective HP is calculated.
Hopefully it is clear that selecting Diablo III gear is a constrained optimization problem. Maybe one day I'll take a stab at writing a program to optimize stats or provide some kind of discussion on the actual tradeoffs between DPS and HP as they relate to killing monsters, but that sounds like a very painful exercise when approximate solutions can be found just by thinking +effective HP and +damage are good.